경사 하강법 (Gradient Descent)

미분

• 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
  

  

  미분식

• sympy.diff로 쉽게 계산 가능

import sympy as sym
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x + 3), x)
Poly(2*x + 2, x, domain='ZZ')

• 함수 f의 주어진 점(x, f(x))에서의 접선의 기울기를 구함
• 접선의 기울기를 이용함으로써 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있음.
  - 미분값이 음수일 경우 x의 값을 왼쪽으로 이동할수록 함수값이 증가
  - 미분값이 양수일 경우 x의 값을 오른쪽으로 이동할수록 함수값이 증가
  

  

• 미분값을 더하면 경사상승법(gradient ascent). 함수의 극대값의 위치 구할 때 사용
• 미분값을 빼면 경사하강법(gradient descent). 함수의 극소값의 위치를 구할 때 사용
• 경사상승법/경사하강법은 모두 극값에 도달하면 움직임을 멈춘다
• Pseudo-code

Input : gradient, init, lr, eps, Output : var
---------------------------------------------
# gradient : 미분을 계산하는 함수
# init : 시작점, lr : 학습률, eps : 알고리즘 종료조건

var = init
grad = gradient(var)
while ( abs(grad) > eps ):
	var = var - lr * grad
    grad = gradient(var)

• Python

def func(val):
	fun = sym.poly(x**2 + 2*x + 3)	// 미분하려는 식 대입
    return fun.subs(x, val), fun
   
def func_gradient(fun, val):
	_, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x, val), diff
    
def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
	cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, init_point)
    while np.abs(diff) > epsilon : 
    	val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
        
    print("함수 : {}, 연산횟수 : {}, 최소점 : ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))

gradient_descent(fun=func, init_point=np.random.uniform(-2, 2))

변수가 벡터일 경우

• 벡터가 input으로 주어지는 다변수함수의 경우, 편미분(partial differentiation)을 사용
  

  

  편미분식

• sympy.diff로 계산 가능

import sympy as sym
from sympy.abc import x, y

sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y), x)

 

• 각 변수별로 편미분을 계산한 gradient 벡터 이용하여 경사하강법/경사상승법에 사용할 수 있음

• pseudo-code

Input : gradient, init, lr, eps, Output : var
---------------------------------------------
# gradient : 그래디언트 벡터를 계산하는 함수
# init : 시작점, lr : 학습률, eps : 알고리즘 종료조건

var = init
grad = gradient(var)
while ( norm(grad) > eps ) :
	var = var - lr * grad
    grad = gradient(var)

• 경사하강법 알고리즘은 그대로 적용되나, 벡터는 절대값 대신 norm을 계산해서 종료조건 설정
• Python

# Multivariate Gradient Descent
def eval_(fun, val):
	val_x, val_y = val
    fun_eval = fun.subs(x, val_x).subs(y, val_y)
    return fun_eval
    
def func_multi(val):
	x_, y_ = val
    func = sym.poly(x**2 + 2*y**2)
    return eval_(func, (x_, y_)), func
    
def func_gradient(fun, val):
	x_, y_ = val
    _, function = fun(val)
    diff_x = sym.diff(function, x)
    diff_y = sym.diff(function, y)
    grad_vec - np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype=float)
    return grad_vec, [diff_x, diff_y]
    
def gradient_descent(fun, init_point, lr_rate = 1e-2, epsilon = 1e-5) :
	cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, val)
    while np.linalg.norm(diff) > epsilon:
    	val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
        
    print("함수 : {}, 연산횟수 : {}, 최소점 : ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))
    
pt = (np.random.uniform(02, 2), np.random.uniform(-2, 2)]
gradient_descent(fun=func_multi, init_point=pt)

 

경사하강법으로 선형회귀 계수 구하기

• 무어-펜로즈는 선형일 때만 사용 가능 / 선형회귀모델은 비선형에서도 사용 가능
• 선형회귀의 목적식은 L2-norm(||y-Xβ||) 이고, 이를 최소화하는 β를 찾아야함.
  

  

• 계산의 편리 위해 L2-norm(||y-Xβ||)를 제곱한 값을 사용.
  

  

• 최종적으로 구해지는 β의 식은

경사하강법 기반 선형회귀 알고리즘

• Pseudo-code

Input : 선형 모델 X, 정답 y, 학습률 lr, 학습 횟수 T, Output : beta
------------------------------------------------------------------
# norm : L2-norm을 계산하는 함수

for t in range(T):
	error = y - X @beta
    grad = - transpose(X) @ error
    beta = beta - lr * grad

• Moore-Penrose처럼 정확한 값에 도달할 때까지 진행하는 것이 아니기 때문에 적절한 학습률과 학습횟수를 선택할 경우에만 수렴 보장됨
• 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있어 수렴이 항상 보장되지는 않음
• Python

X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(x, np.array([1, 2])) + 3

beta_gd = [10.1, 15.1, -6.5] # [1, 2, 3]이 정답
X_ = np.array([np.append(x, [1]) for x in X]) # intercept항 추가

for t in range(5000) : # T를 5000으로 둠
	error = y - X_ @ beta_gd
    # error = error / np.linalg.norm(error)
    grad = -np.transpose(X_) @ error
    beta_gd = beta_gd - 0.01 * grad
    
print(beta_gd)

• 이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해서는 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있음.
• 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 경사하강법을 사용한다고 했을 때 수렴이 항상 보장되지 않음. 이를 해결하기 위해 확률적 경사하강법을 사용

확률적 경사하강법 (stochastic gradient descent)

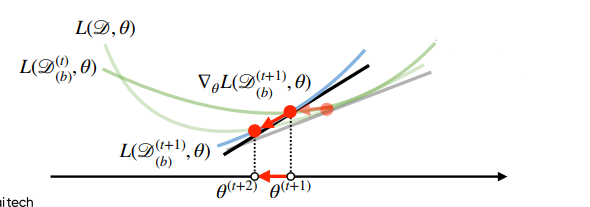
• 모든 데이터를 사용하는 경사하강법과 달리, 확률적 경사하강법은 데이터 한개, 또는 데이터의 일부(mini-batch)를 활용하여 업데이트함
• non-convex 목적식은 SGD를 통해 최적화할 수 있음
• 데이터를 모두 사용하는 경사하강법과는 달리, 데이터의 일부를 가지고 parameter를 update하기 때문에 연산자원을 효율적으로 활용 가능
• 미니배치는 데이터를 확률적으로 선택하므로 매번 목적식의 모양이 바뀜
• 값은 다를 수 있으나, 방향은 같을 것으로 기대함
  • 연산량이 b/n으로 감소
  • 목적식의 gradient를 근사해서 계산

경사하강법 vs 확률적 경사하강법

경사하강법 vs 확률적 경사하강법

• 경사하강법에 비해 확률적 경사하강법의 메모리 효율이 높고, 적은 시간에 결과를 찾아낼 수 있음