Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- 데이터사이언스
- 부스트캠프
- 데이터과학
- 자바
- 소프티어
- 알고리즘
- 클린코드 파이썬
- data science methodology
- Python
- 티스토리챌린지
- string
- 코세라
- softeer
- 코딩테스트
- 코테
- Java
- 파이썬
- 문자열
- 데이터 사이언스
- Coursera
- 클린코드
- Boostcamp AI
- 깨끗한 코드
- Clean Code
- IBM
- programmers
- AI Mathematics
- 오블완
- Data Science
- 프로그래머스
Archives
- Today
- Total
떼닝로그
베이즈 통계학 본문
조건부 확률
- 사건 B가 일어난 상황에서 사건 A가 발생할 확률 P(A∩B) = P(B)P(A|B)
- 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려줌
- A라는 새로운 정보가 주어졌을 때 P(B)로부터 P(B|A)를 계산하는 방법 제공

- A라는 새로운 정보가 주어졌을 때 P(B)로부터 P(B|A)를 계산하는 방법 제공
예제를 통한 베이즈 정리의 이해
- 아래는 베이즈 정리를 위한 식
- θ : model에서 계산하고 싶어하는 parameter(모수). hypothesis
- \(D\) : 새로 관찰하는 data
- 사후확률 : data가 주어져있을 때 parameter θ가 성립할 확률
- 사전확률 : modeling 전 사전에 주어진 확률
- 가능도(likelihood) : 현재 주어진 parameter(모수)를 가정해서 이 data가 관찰될 확률 계산
- Evidence : data 자체의 분포

예제 1
COVID-99의 발병률이 10%라고 하자. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1%라고 할 때 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99에 감염되었을 확률은?
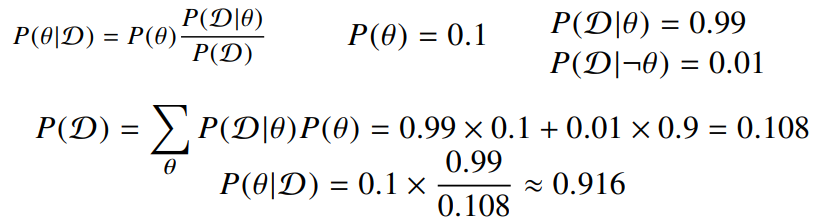
- \(D\) : 검진 경우
- θ : 실제로 걸렸을 때의 상황
- P(\(D\)) : evidence의 확률
- 이때, P(D|¬θ)를 모르면 이러한 문제 풀기 어려워지게 됨
예제 2
COVID-99의 발병률이 10%라고 하자. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 10%라고 할 때 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99에 감염되었을 확률은?

- 병에 실제로 걸렸을 때 검진될 확률이 99%더라도, 실제로 걸리지 않았을 때 오검진될 확률이 다름
조건부 확률의 시각화 (Confusion Matrix)

- True Positive : 양성일 때 실제로도 양성일 경우
- False Positive : 양성이 나왔으나 실제로는 음성일 경우
- False Negative : 음성 나왔으나 실제로는 양성일 경우
- True Negative : 음성이 나왔을 때 실제로도 음성일 경우
베이즈 정리를 통한 정보의 갱신
- 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있음

조건부 확률 -> 인과관계?
- 조건부 확률은 유용한 통계적 해석을 제공하나, 인과관계(causality)를 추론할 때 함부로 사용해선 안됨
- 인과관계는 데이터 분포의 변화에 강건한 예측모형 만들 때 필요
- 조건부확률 기반 예측모형은 시나리오에 따라 예측확률이 크게 변할 수 있음
- 인과관계 기반 예측모형은 높은 예측 정확도를 기대하면 안 됨. data 분포에 대해 경건한 예측모형은 가능.

- 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야.
- 중첩요인을 제거하지 않을 경우, 가짜 연관성(spurious correlation) 나옴'
예제 1
Z가 신장 결석 크기, T가 치료법, R이 완치 정도라고 했을 때, 치료법 a와 b 중 어느 것이 더 나은가?

- 전체적으로 봤을 땐 치료법 b, 각각 봤을 땐 치료법 a가 더 나음
- '크기에 따른' 중첩효과 제거해야 함
치료법 A를 선택했을 경우
- do(T=a)라는 조정(intervention) 효과를 통해 Z의 개입 제거
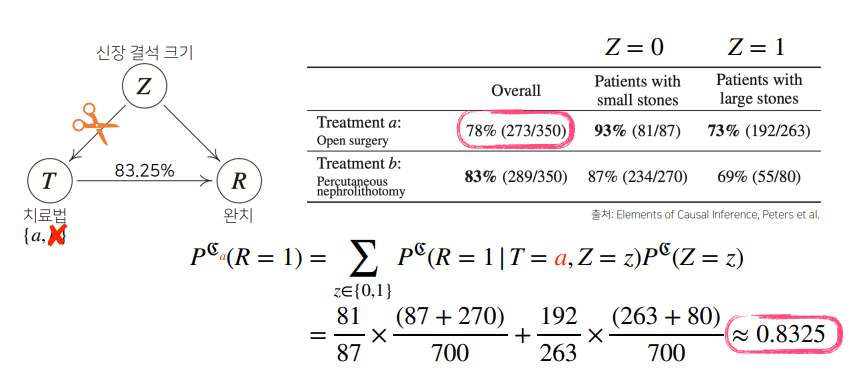
치료법 B를 선택했을 경우
- 인과관계로 계산한 확률은 조건부확률로 계산한 치료효과와 정반대의 결과가 나옴

'Boostcamp AI Tech > AI Mathematics' 카테고리의 다른 글
| RNN 기초 (0) | 2022.06.21 |
|---|---|
| CNN 기초 (0) | 2022.06.18 |
| 통계학 기초 (0) | 2022.06.17 |
| 확률론 기초 (0) | 2022.06.16 |
| 딥러닝 학습방법 이해하기 (0) | 2022.06.16 |
Comments




