Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- 파이썬
- 코세라
- 코딩테스트
- Coursera
- IBM
- string
- 클린코드 파이썬
- 부스트캠프
- softeer
- 티스토리챌린지
- 데이터 사이언스
- programmers
- 깨끗한 코드
- 자바
- 알고리즘
- 프로그래머스
- 소프티어
- 코테
- data science methodology
- 데이터사이언스
- 데이터과학
- AI Mathematics
- Clean Code
- Data Science
- 클린코드
- Python
- Boostcamp AI
- 문자열
- 오블완
- Java
Archives
- Today
- Total
떼닝로그
딥러닝 학습방법 이해하기 본문
Softmax 연산
- 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
- 출력물의 모든 값을 고려함
- 분류(classification) 문제를 풀 때 선형모델과 softmax 함수 결합하여 특정 vector가 어떤 class에 속할 확률 예측

def softmax(vec):
# denumerator : 각 출력 vector
denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True) # np.max 사용함으로써 overflow 방지
# numerator : 각 출력 vector들의 합에 exponential 연산 수행
numerator = np.sum(denumerator, axis=-1, keepdims=True)
val = denumerator / numerator
return val- 학습에는 softmax를 사용하고, 추론에서는 one-hot vector로 최대값을 가진 주소만 1로 출력하는 연산 사용
활성함수(activation function)
- 활성함수는 실수 차원 위에 정의된 비선형 함수
- 활성함수를 사용하지 않으면 딥러닝은 선형모형과 차이가 없게 됨
- 해당 주소에 있는 출력값만을 고려함 (softmax는 출력물의 모든 값을 고려함)
- 선형 모델 -> 비선형모델 변환 가능
- 대표적인 예시로는 sigmoid 함수, hyperbolic tangent 함수, ReLU 함수

신경망을 수식으로 분해해보자
- 신경망은 선형모델과 활성함수(activation function)을 합성한 함수. 비선형모델

행렬로 표한한 신경망 - 데이터가 바뀌면 결과값도 바뀌게 됨. 이에 따라 출력 벡터의 차원은 d에서 p로 바뀜
- O : 출력값
- X : 전체 data. 각각의 data point들로 이루어진 행들로 구성
- W : 가중치 행렬. data들의 point를 출력으로 뱉어주는 행렬. data를 다른 공간으로 보내주는 역할 함.
- b : y절편. 각 행들이 전부 같은 값을 가지게 됨. (nxd) x (dxp)으로 출력으로 나오는 값과 같은 차원이어야 함
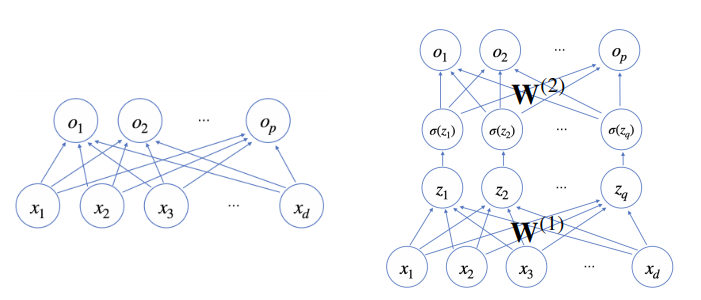
- x와 o를 이어주는 선은 (dxp) 차원의 가중치행렬 W. 이를 통해 출력 벡터의 차원이 바뀜
- 선형모델의 결과물인 o에 softmax 함수를 합성하면 확률벡터가 되므로 특정 클래스 k에 속할 확률로 해석 가능
- z는 변형시킨 vector를 잠재(hidden) vector인 Neuron으로 나타낸 것.
- σ는 활성함수를 나타냄.

- 활성함수 σ는 잠재벡터 z의 각 노드에 개별적으로 적용하여 새로운 잠재벡터 H를 만듦
- 잠재벡터 H에서 가중치 행렬 W와 b를 통해 다시 한 번 선형변환해서 출력하게 되면 (W2, W1)를 parameter로 가진 2층 신경망이 나옴
다층 퍼셉트론 (Multi Layer Perceptron)
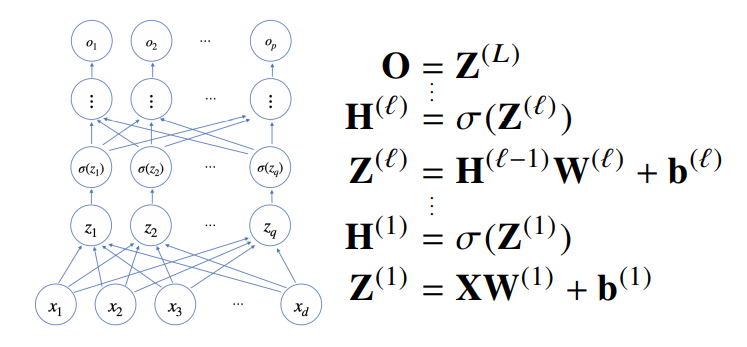
- 다층(multi-layer) 퍼셉트론(MLP)는 신경망이 여러 층 합성된 함수
- MLP의 parameter는 L개의 가중치 행렬 W(L), ..., W(1)로 이루어져 있음
- 다층 구조를 이용함으로써 임의의 연속함수 근사 가능
- 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 빨리 줄어들어 효율적인 학습 가능
- 적은 parameter로 훨씬 더 복잡한 함수 표현 가능
- 층이 얇으면 필요한 뉴런의 숫자가 기하급수적으로 늘어나기 때문에 넓은(wide) 신경망이 되어야 함
- l = 1, 2, ... , L까지 순차적인 신경망 계산을 순전파(forward propagation)
역전파 알고리즘 (backpropagation)
- 더 많은 parameter들에 대해 경사하강법 적용
- 각 층에서 계산된 gradient가 아래층으로(역순) 전달되면서 gradient 값 update
- 손실함수가 L일 때, 역전파는 σL / σW(l) 정보를 계산할 때 사용. 각각의 가중치 행렬에 대해 손실함수 미분
역전파 알고리즘 vs 순전파 알고리즘
- 순전파 알고리즘(forward propagation)은 입력을 받아서 선형모델과 활성화 함수를 반복적으로 수행하는 연산
- 역전파 알고리즘이 순전파 알고리즘에 비해 memory 사용량이 많음
- 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation) 사용

'Boostcamp AI Tech > AI Mathematics' 카테고리의 다른 글
| 통계학 기초 (0) | 2022.06.17 |
|---|---|
| 확률론 기초 (0) | 2022.06.16 |
| 경사 하강법 (Gradient Descent) (1) | 2022.06.15 |
| 행렬 (Matrix) (0) | 2022.04.04 |
| 벡터 (Vector) (0) | 2022.04.04 |
Comments




