Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
Tags
- Java
- Clean Code
- 파이썬
- 데이터 사이언스
- 데이터사이언스
- programmers
- Boostcamp AI
- 부스트캠프
- 알고리즘
- 데이터과학
- Coursera
- 코세라
- 코테
- softeer
- string
- Python
- 문자열
- 티스토리챌린지
- 깨끗한 코드
- AI Mathematics
- 오블완
- 자바
- 클린코드
- Data Science
- 클린코드 파이썬
- 프로그래머스
- 소프티어
- data science methodology
- 코딩테스트
- IBM
Archives
- Today
- Total
떼닝로그
행렬 (Matrix) 본문
행렬
- 행렬(matrix)는 벡터를 원소로 가지는 2차원 배열
- 행(row)과 열(column)으로 이뤄져있음
- 행렬의 특정 행(또는 열)을 고정하면 행(또는 열)벡터
- 행렬의 행벡터 x_i는 i번째 데이터
- 행렬의 x_ij는 i번째 데이터의 j번째 변수의 값
행렬의 계산
- 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈 계산 가능
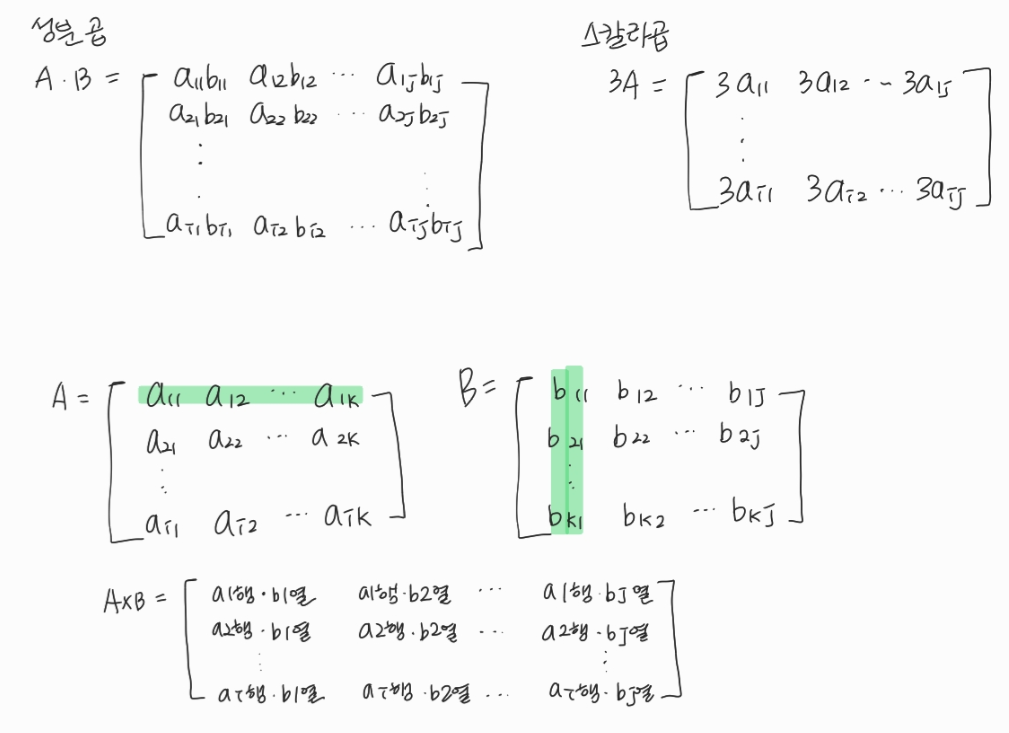
- 성분곱은 벡터와 같음. A_ij * B_ij으로 하나씩 곱하는 방식
- 스칼라곱도 벡터와 같음. 3A = A의 행렬 모든 원소에 스칼라값인 3을 곱해주면 됨
- 행렬 곱셈은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬 계산
- 행렬 곱셈 위해서는 두 개의 행렬 사이 차원이 같아야함. ex) A(NxK) * B(KxM)
- 행렬 곱셈 이용하여 벡터를 다른 차원의 공간으로 보낼 수 있음
- 행렬 곱셈 이용하여 패턴 추출, 데이터 압축 가능
행렬의 내적
- numpy.inner 사용하여 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬 계산 가능
> X = np.array([[1, -2, 3], [7, 5, 0], [-2, -1, 2]]) > Y = np.array([[0, 1, -1], [1, -1, 0]]) > np.inner(X, Y) array([[-5, 3], [5, 2], [-3, -1]])
역행렬 (inverse matrix)
- 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix).
- A의 역행렬은 A^−1로 표현
- 역행렬은 행과 열 숫자가 같고(NxN 행렬), 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
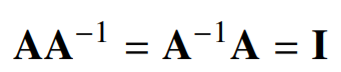
- numpy.linalg.inv 이용
> X = np.array([[1, -2, 3], [7, 5, 0], [-2, -1, 2]]) > np.linalg.inv(X) array([[0.21276596, 0.0212766, -0.31914894], [-0.29787234, 0.17021277, 0.44680581], [0.06382979, 0.10638298, 0.40425532]]) - 역행렬을 구할 수 없을 땐 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 A^+ 이용
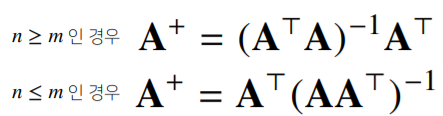
- numpy.linalg.pinv 이용
> A = np.array([[0, 1], [1, -1], [-2, 1]]) > np.linalg.pinv(A) array([[5.00000000e-01, 4.09730229e-17, -5.00000000e-01], [8.33333333e-01, -3.33333333e-01, -1.66666667e-01]]) - numpy.linalg.pinv 이용하여 연립방정식의 해, 선형회귀식 등을 구할 수 있음
'Boostcamp AI Tech > AI Mathematics' 카테고리의 다른 글
| 통계학 기초 (0) | 2022.06.17 |
|---|---|
| 확률론 기초 (0) | 2022.06.16 |
| 딥러닝 학습방법 이해하기 (0) | 2022.06.16 |
| 경사 하강법 (Gradient Descent) (1) | 2022.06.15 |
| 벡터 (Vector) (0) | 2022.04.04 |
Comments





